
递归:将问题分解成子问题求解,从较小的问题逐渐逼近原始问题,很多时候只需要在f(n-1)中加入或移除某些东西或稍作修改就可以求得f(n)
动态规划与递归的区别:动态规划要将中间的结果缓存起来以备后续使用
1、斐波那契数列问题
public class fibonacci { private final static int max=1000; /** * 递归方法,时间复杂度2^i * @param i * @return */ public static long recursion(int i) { if (i == 0) return 0; if (i == 1) return 1; return recursion(i - 1) + recursion(i - 2); } private static long[] temp=new long[max]; /** * 动态规划方法,将中间结果缓存起来,时间复杂度 i * @param i * @return */ public static long dynamic(int i){ if (i == 0) return 0; if (i == 1) return 1; if(temp[i]!=0){ return temp[i]; } temp[i]=dynamic(i-1)+dynamic(i-2); return temp[i]; } public static void main(String[]args) { long startTime = System.currentTimeMillis(); // 获取开始时间 System.out.println(recursion(40)); long endTime = System.currentTimeMillis(); // 获取结束时间 System.out.println("程序运行时间: " + (endTime - startTime) + "ms"); long startTime2 = System.currentTimeMillis(); // 获取开始时间 System.out.println(dynamic(40)); long endTime2 = System.currentTimeMillis(); // 获取结束时间 System.out.println("程序运行时间: " + (endTime2 - startTime2) + "ms"); }} 运行结果
102334155
程序运行时间: 1145ms
102334155
程序运行时间: 0ms
递归算法的空间效率很低,每次递归调用都会在栈上增加一层
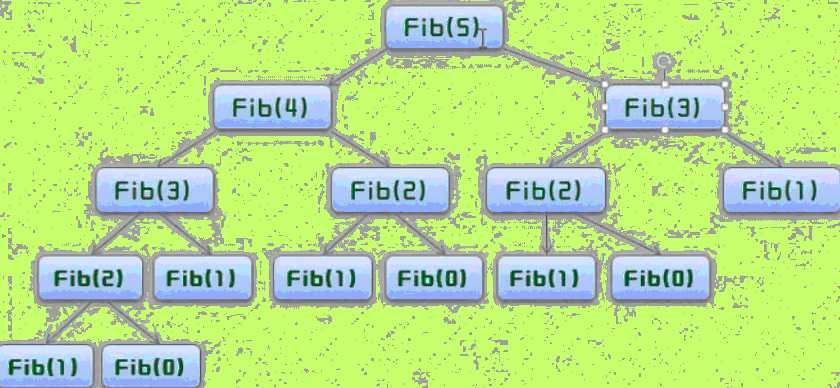
参考:
扩展:
用8个1*2的小长条去覆盖一个2*8的棋盘,要求完全覆盖棋盘,小长条彼此不重叠。求总共有多少总覆盖方法。
其实就是fibonacci数列
分析见
2、楼梯问题
楼梯有n阶台阶,一次可以上1阶,2阶,或3阶,计算有多少种上楼梯的方式
小孩上完楼梯最后一步即抵达第n阶的那一步,可能走1阶或2阶或3阶,最后一步可能是第n-1阶向上走1,或n-2向上走2,或n-3向上走3,同样用递归问题可以解决
public class stair { public static int getMethods(int num) { if (num<0) { return 0; } if (num==0) { return 1; } return getMethods(num-1)+getMethods(num-2)+getMethods(num-3); } public static void main(String[] args) { System.out.println(getMethods(6)); }} 输出结果为:
24
扩展:
用1分、2分和5分的硬币凑成1元,共有多少种不同的凑法?(华为机试题)
参考:
这个不能用上述方法,因为走楼梯不同顺序是不同的走法,而硬币的凑法则与顺序无关,写程序可用穷举法
public class coin { public static int getKinds(){ int num=0; for (int i = 0; i < 21; i++) { for (int j = 0; j <= 100-5*i; j++) { for (int k = 0; k <= 100-5*i-2*j; k++) { if(5*i+2*j+k==100){ num++; } } } } return num; } public static void main(String[] args) { System.out.println(getKinds()); }} 输出:
541